来る5月20日には総会が開かれますが、総会の後に下記の要領で講演会が開かれます。

日時：平成29年5月20日（土）午後3時から4時
場所：池袋立教中学校・高等学校　4階地学実験室
講師：細矢治夫（お茶の水女子大学名誉教授）
タイトル：
「化学と数学をつなげる折り紙と封筒」

「化学と数学」と聞くと、「えっ、科学じゃなくて化学なの、数学とは結びつかないなー」と思われる方が多いと思います。でも違うんです。

高校の化学で、メタン、エタン、プロパン、ブタン、ペンタン、、と、やみくもに覚えたことがあると思います。炭素原子が１から順に増えていくアルカンの名前ですね。炭素原子数が6の時はヘキサンです。

ヘキサンの分子式はC6H12で、次のような直鎖状の分子です。
ヘキサンには、3－メチルペンタン、2－メチルペンタン、2,3－ジメチルブタン、2,2－ジメチルブタンの4つの構造異性体があり、それぞれ、上の述べた順に次のような構造をしています。
　同じ分子式ですが、形の異なるそれぞれの分子では沸点が異なります。何となく、小さくまとまっている方が、沸点が低い気がしますが、それをどうやって表現すればいいでしょうか。そこでトポロジカル・インデックス（Topological Index、Z）（Hosoya indexとも言います）が登場します。Zは次のように定義される記述子です。

N個の炭素原子をそれぞれ点と考えて表したグラフGで、2点間の最小単位を隣接させずにいくつ置けるかを数え【非隣接数　P（G，ｋ）で表す】、最小単位の数ｋを増やしていってPの合計を求めたものがZになります。ただしｋ＝0の時は１と定義します。

たとえば、炭素数5のペンタンでは、ｋ＝1の時は点の間は4つありますから、P＝４になり、ｋ＝２の時は次のようになるので、P=3になります。
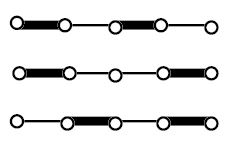ｋ＝２で打ち止めなので、Pを合計したZは1+4+3＝8になります。

ペンタンで述べた方式でヘキサンのZを求めて、沸点との関係をグラフにすると次のようになり、きれいに直線に載ります。上で述べた「何となく」が、Zという記述子で数量的に関係づけられたわけです。

もう一つ、生成熱との関係を同じようにグラフで求めても、沸点の場合と同じように（傾きは逆ですが）、きれいに直線に乗ります。

　このように、化学に理論と数理的な裏付けを持ち込もうとして考え出したトポロジカル・インデックスは、フィボナッチ数列と結びつき、さらにさまざまな数学的な分野に適用が広がっています。

でもって、化学と数学をつなげる折り紙と封筒ということになるのですが、それは当日実演と実習までのお楽しみにしておいてくださいね。

Hosoya cube

ユニット折り紙からできる多面体等を、実演付きで紹介します。

花の時が足早に過ぎ去り、さわやかの5月の声を聴く頃になりました。会員各位におかれましては、充実した時をお過ごしのことと思います。

さて、新しい年度が4月から始まって1か月が過ぎました。昨年度の決算及び今年度の活動方針と予算、ならびに理事・監事の改選を決める定例の総会を、下記のとおり開催いたします。ご参加くださるようお願いいたします。

日時：2017年5月20日（土）午後2時から3時
場所：立教池袋中学校・高等学校　地学実験室（4階）
（東京都豊島区西池袋５-１６-５）

詳しい通常総会取集の通知及び資料は追って郵送いたします。出席される場合は、同封の議案書の出欠欄に出席のしるしを付して同封の返信用封筒（切手貼付済み）でご返送ください。

万一、ご欠席の場合は、議案書により、委任をするか、それぞれの議案に対して議決権を行使するかそれぞれの欄にしるしを付して同封の返信用封筒（切手貼付済み）でご返送ください。総会はSSISSの意思決定会議であり、定款により定足数がありますので、お忘れにならないようにお願いいたします。

総会の後に、細矢治夫会員による実習付きの講演会が行われます。タイトルは「化学と数学をつなげる折り紙と封筒」という魅力的なものです。どんなお話が聞けるか楽しみですね。

さらにこの後には、懇親会を開催します。といっても大げさなものではなく、近くの飲み屋さんで、楽しくワイワイと懇親を深める予定になっています。

というわけで総会にはぜひご参加ください。

また総会案内の封筒内には、今年度の「会費納入のお願い」の文書と振替用紙が同封されています。文書中の手順に従って会費の納入をお願いいたします。